《2023屆高考一輪復(fù)習(xí) 練習(xí)12 二次函數(shù)與冪函數(shù)(Word版含答案)》由會員分享�����,可在線閱讀��,更多相關(guān)《2023屆高考一輪復(fù)習(xí) 練習(xí)12 二次函數(shù)與冪函數(shù)(Word版含答案)(5頁珍藏版)》請在裝配圖網(wǎng)上搜索����。
1、2023屆高考一輪復(fù)習(xí) 練習(xí)12 二次函數(shù)與冪函數(shù)
一���、選擇題(共10小題)
1. 已知冪函數(shù) fx 的圖象經(jīng)過點 2,22���,則 f4 的值為 ??
A. 12 B. 116 C. 16 D. 2
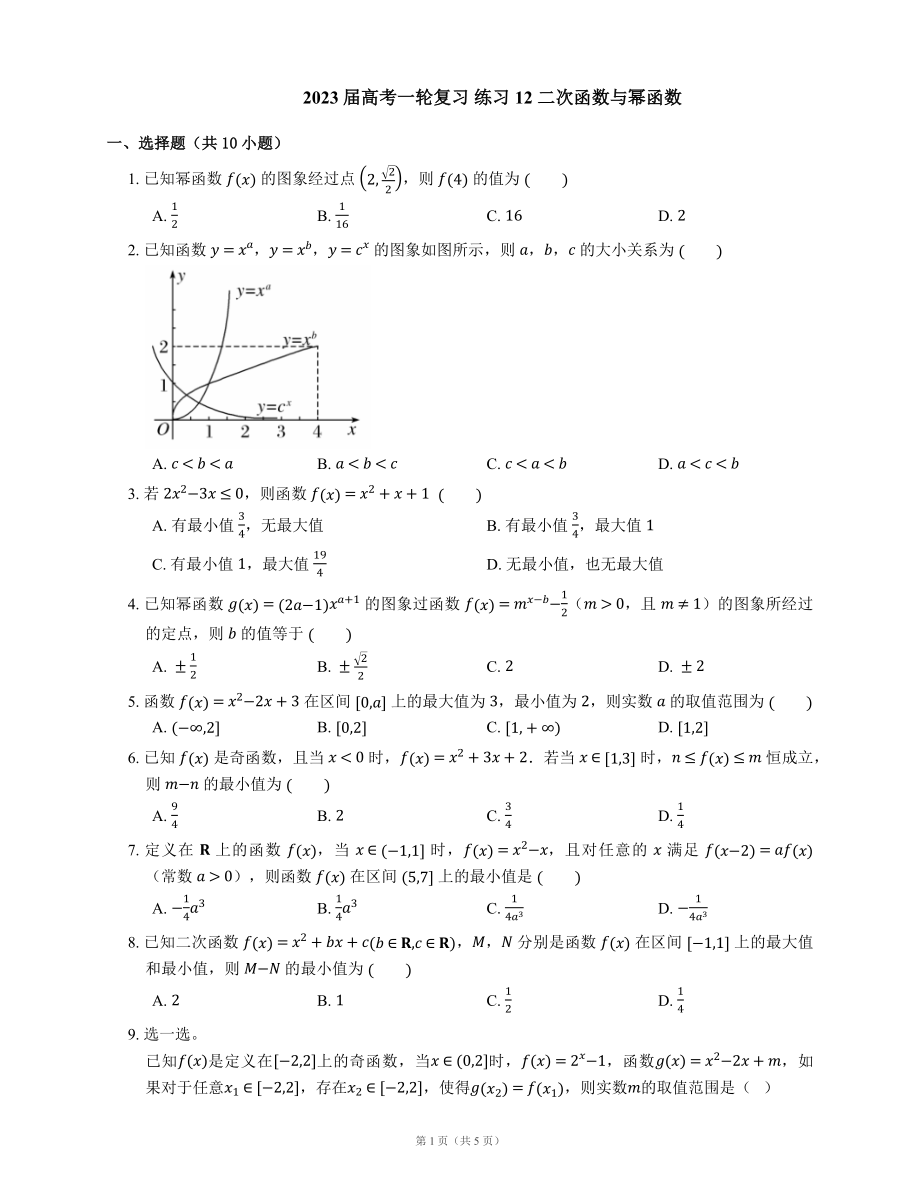
2. 已知函數(shù) y=xa����,y=xb���,y=cx 的圖象如圖所示�����,則 a�����,b�,c 的大小關(guān)系為 ??
A. c
2���、小值,也無最大值
4. 已知冪函數(shù) gx=2a?1xa+1 的圖象過函數(shù) fx=mx?b?12(m>0,且 m≠1)的圖象所經(jīng)過的定點����,則 b 的值等于 ??
A. ±12 B. ±22 C. 2 D. ±2
5. 函數(shù) fx=x2?2x+3 在區(qū)間 0,a 上的最大值為 3,最小值為 2���,則實數(shù) a 的取值范圍為 ??
A. ?∞,2 B. 0,2 C. 1,+∞ D. 1,2
6. 已知 fx 是奇函數(shù)���,且當(dāng) x<0 時,fx=x2+3x+2.若當(dāng) x∈1,3 時���,n≤fx≤m 恒成立���,則 m?n 的最小值為 ??
A. 94 B. 2 C. 34
3、 D. 14
7. 定義在 R 上的函數(shù) fx�����,當(dāng) x∈?1,1 時�����,fx=x2?x��,且對任意的 x 滿足 fx?2=afx(常數(shù) a>0),則函數(shù) fx 在區(qū)間 5,7 上的最小值是 ??
A. ?14a3 B. 14a3 C. 14a3 D. ?14a3
8. 已知二次函數(shù) fx=x2+bx+cb∈R,c∈R���,M����,N 分別是函數(shù) fx 在區(qū)間 ?1,1 上的最大值和最小值����,則 M?N 的最小值為 ??
A. 2 B. 1 C. 12 D. 14
9. 選一選。
已知f(x)是定義在[?2,2]上的奇函數(shù)�,當(dāng)x∈(0,2]時,f(x)=2x?1���,函數(shù)
4���、g(x)=x2?2x+m,如果對于任意x1∈[?2,2]���,存在x2∈[?2,2]����,使得gx2=fx1��,則實數(shù)m的取值范圍是( )
A. (?∞,?2) B. (?5,?2) C. [?5,?2] D. (?∞,?2]
10. 函數(shù) fx=x∣x∣?1 在 m,n 上的最小值為 ?14,最大值為 2����,則 n?m 的最大值為 ??
A. 52 B. 52+22 C. 32 D. 2
二����、選擇題(共2小題)
11. 設(shè)函數(shù) fx=ax2+bx+ca≠0,對任意實數(shù) t 都有 f4+t=f?t 成立�,則函數(shù)值 f?1,f1���,f2����,f5 中����,最小的可能是 ??
5、A. f?1 B. f1 C. f2 D. f5
12. 已知函數(shù) fx=x2?2ax+bx∈R���,給出下列命題����,其中是真命題的是 ??
A. 若 a2?b≤0,則 fx 在區(qū)間 a,+∞ 上是增函數(shù)
B. 存在 a∈R����,使得 fx 為偶函數(shù)
C. 若 f0=f2,則 fx 的圖象關(guān)于 x=1 對稱
D. 若 a2?b?2>0�,則函數(shù) hx=fx?2 有 2 個零點
三、填空題(共4小題)
13. 冪函數(shù) fx=m2?3m+3xm 的圖象關(guān)于 y 軸對稱�,則實數(shù) m= ?.
14. 已知函數(shù) fx=x2?2x+3,
6�����、若函數(shù) y=fx?a 在 2,+∞ 上是增函數(shù)�����,則實數(shù) a 的取值范圍是 ?.
15. 已知 fx=x2+2a?1x+2 在 1,5 上的最大值為 f1��,則 a 的取值范圍是 ?.
16. 已知 fx=x+12,x∈0,122x?1,x∈12,2.若存在 x1��,x2�,當(dāng) 0≤x1
7、x?fx?4=afx?2=a2fx?fx?6=afx?4=a3fx,
x∈5,7?x?6∈?1,1�,
fx=1a3fx?6=1a3x?62?x?6=1a3x?6?122?14a3,
當(dāng) x?6=12 時 fx 有最小值為 ?14a3.
8. B
9. C
【解析】∵f(x)是定義在[?2,2]上的奇函數(shù),
∴f(0)=0��,
當(dāng)x∈(0,2]時���,f(x)=2x?1∈(0,3]
則當(dāng)x1∈[?2,2]時,f(x)∈[?3,3]����,
若對于?x1∈[?2,2],?x2∈[?2,2]�����,使得gx2=fx1����,
則等價為g(x)max≥3且g(x)min≤?3,
∵g(x)
8���、=x2?2x+m=(x?1)2+m?1����,x∈[?2,2],
∴g(x)max=g(?2)=8+m�,g(x)min=g(1)=m?1,
則滿足8+m≥3且m?1≤?3����,
解得m≥?5且m≤?2,
故?5≤m≤?2�,
故選:C.
10. B
【解析】當(dāng) x≥0 時,fx=x∣x∣?1=x2?x=x?122?14≥?14��,
當(dāng) x<0 時���,fx=x∣x∣?1=?x2?x=?x+122+14�,
作出函數(shù) fx 的圖象如圖所示.
當(dāng) x≥0 時��,由 fx=x2?x=2����,解得 x=2,
當(dāng) x=12 時����,f12=?14,
當(dāng) x<0 時,由 fx=?x2?x=?14�,
即
9、4x2+4x?1=0��,
解得 x=?4±42+4×42×4=?4±328=?4±428=?1±22�,
所以 x=?1?22,
因為 fx 在 m,n 上的最小值為 ?14����,最大值為 2,
所以 n=2�,?1?22≤m≤12,
所以 n?m 的最大值為 2??1?22=52+22.
11. A����, C����, D
12. A, B
13. 2
14. ?∞,1
15. ?∞,?2
16. ?916
【解析】作出函數(shù)
fx=x+12,x∈0,122x?1,x∈12,2 的圖象如圖所示����,
因為存在 x1,x2�����,當(dāng) 0≤x1
 2023屆高考一輪復(fù)習(xí) 練習(xí)12 二次函數(shù)與冪函數(shù)(Word版含答案)
2023屆高考一輪復(fù)習(xí) 練習(xí)12 二次函數(shù)與冪函數(shù)(Word版含答案)