《2022年高中數(shù)學(課前預習+課初+課中+課末+課后)§1-4 函數(shù)的單調性教案 新人教A版必修1》由會員分享�,可在線閱讀,更多相關《2022年高中數(shù)學(課前預習+課初+課中+課末+課后)§1-4 函數(shù)的單調性教案 新人教A版必修1(3頁珍藏版)》請在裝配圖網(wǎng)上搜索�。
1、2022年高中數(shù)學(課前預習+課初+課中+課末+課后)§1-4 函數(shù)的單調性教案 新人教A版必修1
【課前預習】閱讀教材P27-32完成下面填空
1.設函數(shù)的定義域為����,區(qū)間
如果對于區(qū)間內(nèi)的任意兩個值,,當時����,都有,那么就說在區(qū)間上是 ����,稱為的
如果對于區(qū)間內(nèi)的任意兩個值,�����,當時�,都有,那么就說在區(qū)間上是 �,稱為的
2.對函數(shù)單調性的理解
(1) 函數(shù)的單調性只能在函數(shù)的定義域內(nèi)來討論,所以求函數(shù)的單調區(qū)間,必須先求函數(shù)的定義域;
(2) 函數(shù)單調性定義中
2�����、的���,有三個特征:一是任意性;二是大小�,即�;三是同 屬于一個單調區(qū)間,三者缺一不可���;
(4)關于函數(shù)的單調性的證明�,如果用定義證明在某區(qū)間上的單調性�����,那么就要用嚴格的四個步驟��,即①取值����;②作差;③判號��;④下結論��。但是要注意��,不能用區(qū)間上的兩個特殊值來代替����。而要證明在某區(qū)間上不是單調遞增的,只要舉出反例就可以了���,即只要找到區(qū)間上兩個特殊的,��,若��,有即可���。
(5)函數(shù)的單調性是對某個區(qū)間而言的,所以受到區(qū)間的限制��,如函數(shù)分別在和內(nèi)都是單調遞減的����,但是不能說它在整個定義域即內(nèi)是單調遞減的����,只能說函數(shù)的單調遞減區(qū)間為和
(6)一些單調性的判斷規(guī)則:①若與在定義域內(nèi)都是增函數(shù)(減函數(shù)),那么在其公共
3、定義域內(nèi)是增函數(shù)(減函數(shù))����。②復合函數(shù)的單調性規(guī)則是“異減同增”
【課初5分鐘】課前完成下列練習���,課前5分鐘回答下列問題
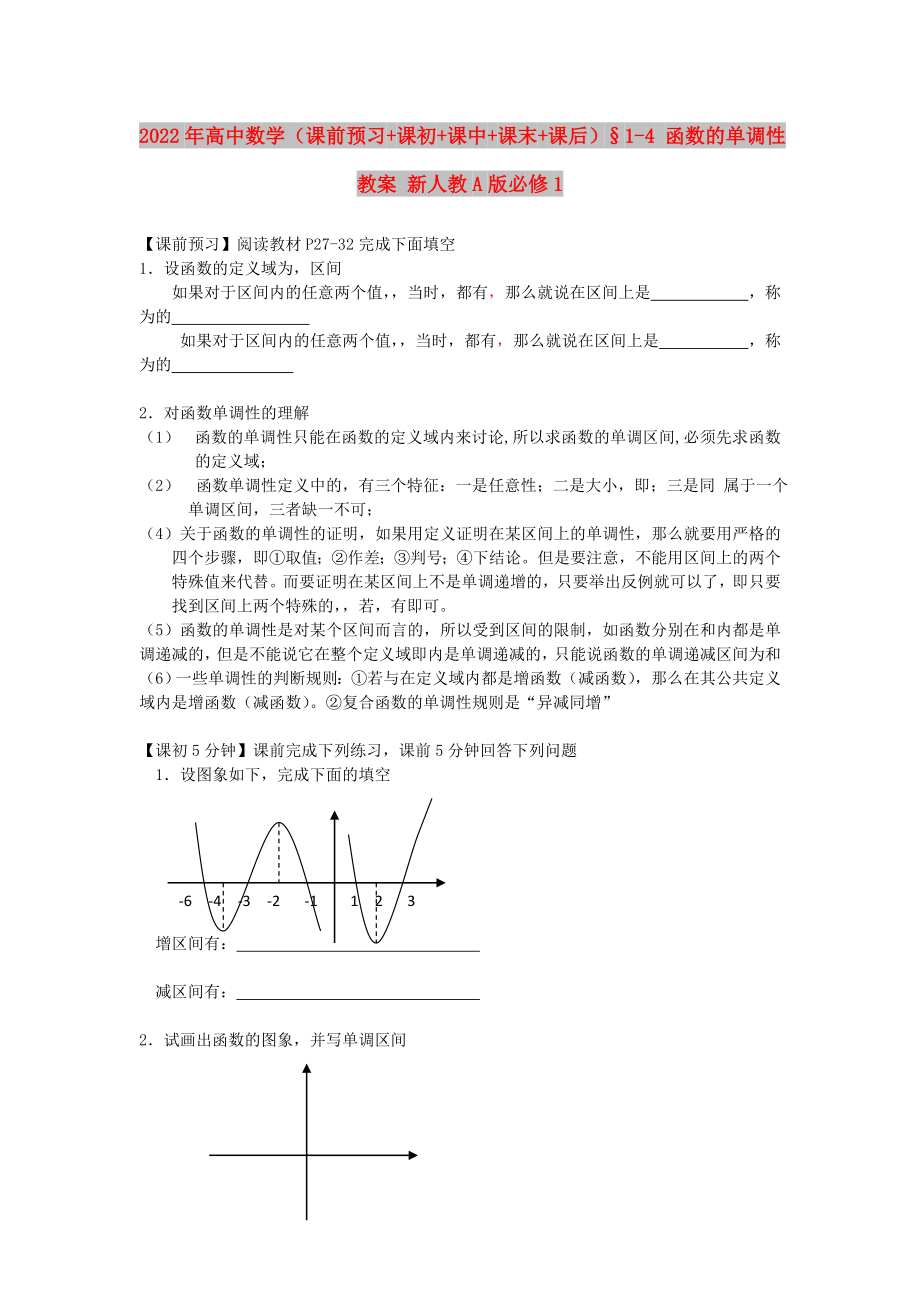
-6 -4 -3 -2 -1 1 2 3
1.設圖象如下�,完成下面的填空
增區(qū)間有:
減區(qū)間有:
2.試畫出函數(shù)的圖象,并寫單調區(qū)間
3. 寫出函數(shù)的單調區(qū)間
強調(筆記):
【課中35分鐘】邊聽邊練邊落實
4.若偶函數(shù)在上是增函數(shù),則下列
關系
4����、式中成立的是
A.
B.
C.
D.
5. 若函數(shù)在上是單調函
數(shù),則的取值范圍是
A. B.
C. D.
6.函數(shù)的單調遞減區(qū)間是____________________
7. 利用函數(shù)的單調性求函數(shù)的值域
8. 求函數(shù)單調遞增區(qū)間
強調(筆記):
【課末5分鐘】 知識整理���、理解記憶要點
1.
2.
3.
5��、
4.
【課后15分鐘】 自主落實����,未懂則問
1.下列函數(shù)中,在區(qū)間上是增函數(shù)的是
A. B.
C. D.
2.已知在區(qū)間上是增函數(shù)�,則的范圍是( )
A. B.
C. D.
3.下列四個命題:(1)函數(shù)在時是增函數(shù),也是增函數(shù),所以是增函數(shù)�����;(2)若函數(shù)與軸沒有交點���,則且����;(3) 的遞增區(qū)間為;(4) 和表示相等函數(shù)����。
其中正確命題的個數(shù)是( )
A. B. C. D.
4.求的單調區(qū)間
5.若在區(qū)間上是增函數(shù)����,則的取值范圍是 ��。
互助小組長簽名:
 2022年高中數(shù)學(課前預習+課初+課中+課末+課后)§1-4 函數(shù)的單調性教案 新人教A版必修1
2022年高中數(shù)學(課前預習+課初+課中+課末+課后)§1-4 函數(shù)的單調性教案 新人教A版必修1