《2020高考數(shù)學(xué)二輪復(fù)習(xí) 分層特訓(xùn)卷 客觀題專練 立體幾何(10) 文》由會員分享���,可在線閱讀,更多相關(guān)《2020高考數(shù)學(xué)二輪復(fù)習(xí) 分層特訓(xùn)卷 客觀題專練 立體幾何(10) 文(8頁珍藏版)》請在裝配圖網(wǎng)上搜索����。
1���、立體幾何(10)
一、選擇題(本題共12小題�,每小題5分,共60分.在每小題給出的四個選項中����,只有一項是符合題目要求的)
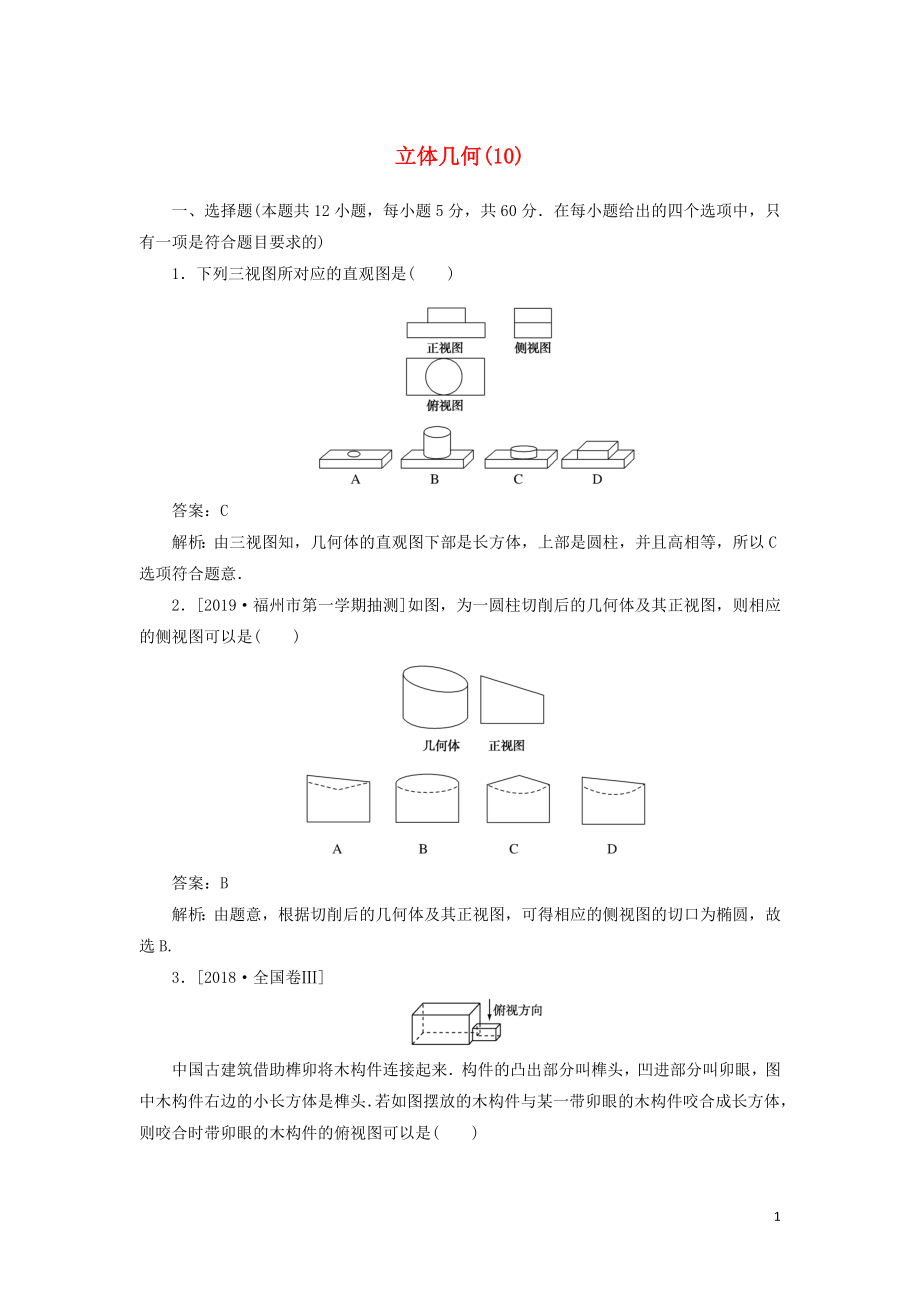
1.下列三視圖所對應(yīng)的直觀圖是( )
答案:C
解析:由三視圖知,幾何體的直觀圖下部是長方體����,上部是圓柱,并且高相等��,所以C選項符合題意.
2.[2019·福州市第一學(xué)期抽測]如圖���,為一圓柱切削后的幾何體及其正視圖���,則相應(yīng)的側(cè)視圖可以是( )
答案:B
解析:由題意,根據(jù)切削后的幾何體及其正視圖���,可得相應(yīng)的側(cè)視圖的切口為橢圓���,故選B.
3.[2018·全國卷Ⅲ]
中國古建筑借助榫卯將木構(gòu)件連接起來.構(gòu)件的凸出部分叫榫頭����,凹進部分叫卯眼���,圖中
2���、木構(gòu)件右邊的小長方體是榫頭.若如圖擺放的木構(gòu)件與某一帶卯眼的木構(gòu)件咬合成長方體,則咬合時帶卯眼的木構(gòu)件的俯視圖可以是( )
A
B
C
D
答案:A
解析:
由題意可知帶卯眼的木構(gòu)件的直觀圖如圖所示�,由直觀圖可知其俯視圖應(yīng)選A.
故選A.
4.[2019·桂林、百色���、崇左市聯(lián)合模擬]如圖����,在正方體ABCD-A1B1C1D1中��,E為棱BB1的中點�,用平面AEC1截去該正方體的上半部分,則剩余幾何體的正(主)視圖為( )
答案:B
解析:因為ABCD-A1B1C1D1是正方體�����,所以AE∥平面DCC1D1�,設(shè)平面AEC1∩平面DCC1D1=C1G,
3�、因為AE?平面AEC1,所以AE∥C1G�����,AE=C1G.取CC1的中點F����,連接EF,DF����,易得四邊形AEFD為平行四邊形,所以AE∥DF�����,AE=DF�����,所以C1G∥DF���,C1G=DF��,所以G為DD1的中點�,連接AG,則平面AEC1G即平面AEC1截正方體所得的截面�,則剩余的幾何體為 A1B1C1D1GAE,所以易得其正視圖如選項B所示�,故選B.
5.[2019·武漢調(diào)研]某幾何體的三視圖如圖所示,則從該幾何體的所有頂點中任取兩個頂點���,它們之間距離的最大值為( )
A. B.
C.2 D.2
答案:B
解析:
由三視圖知�����,該幾何體是一個四棱柱��,記為四棱柱ABCD-A1B1
4��、C1D1���,將其放在如圖所示的長方體中,底面ABCD是邊長為1的正方形�����,四棱柱的高為1,連接AC1��,觀察圖形可知����,幾何體中兩頂點間距離的最大值為AC1的長��,即=.故選B.
6.設(shè)一個球形西瓜���,切下一刀后所得切面圓的半徑為4��,球心到切面圓心的距離為3�,則該西瓜的體積為( )
A.100π B.π
C.π D.π
答案:D
解析:因為切面圓的半徑r=4���,球心到切面的距離d=3����,所以球的半徑R===5���,故球的體積V=πR3=π×53=π�,即該西瓜的體積為π.
7.[2019·昆明市質(zhì)量檢測]一個幾何體的三視圖如圖所示��,則該幾何體的體積為( )
A.4+ B.4+
C.12
5、+ D.12+
答案:C
解析:三視圖對應(yīng)的幾何體是一個半球與一個長方體的組合體��,半球的半徑為1����,體積為;長方體的長�、寬、高分別為2�����、2�、3,體積為12.所以組合體的體積為12+.故選C.
8.[2019·廣東省七校聯(lián)考]某幾何體的三視圖如圖所示���,則該幾何體的表面積和體積分別是( )
A.24+6和40 B.24+6和72
C.64+6和40 D.64+6和72
答案:C
解析:
把三視圖還原成幾何體��,如圖所示.由題意知S四邊形ABCD=12�����,S四邊形BCC1B1=8����,S四邊形ABB1A1=6,S四邊形ADSA1=(2+6)×4×=16���,S四邊形DCC1S=(2
6�、+6)×3×=12.易得B1A1⊥SA1�����,B1C1⊥SC1�,且SA1=4���,SC1=5���,所以S△SA1B1=3×4×=6,S△SB1C1=4×5×=10��,所以該幾何體的表面積為12+8+6+16+12+6+10=64+6.在棱SD上取一點D1���,使得DD1=2���,連接A1D1,C1D1,則該幾何體的體積V=VS-A1B1C1D1+VABCD-A1B1C1D1=×12×4+12×2=40���,故選C.
9.[2019·廣州市綜合檢測(一)]一個幾何體的三視圖如圖所示���,其中正視圖和俯視圖中的四邊形是邊長為2的正方形,則該幾何體的表面積為( )
A. B.7π
C. D.8π
答案:B
解
7�����、析:由三視圖可知該幾何體是一個圓柱體和一個球體的四分之一的組合體��,則所求的幾何體的表面積為×4π×12+π×12+π×12+2π×1×2=7π�,選B.
10.[2019·蓉城名校第一次聯(lián)考]已知一個幾何體的正視圖和側(cè)視圖如圖1所示,其俯視圖用斜二測畫法所畫出的水平放置的直觀圖是一個直角邊長為1的等腰直角三角形(如圖2所示)�����,則此幾何體的體積為( )
A.1 B.
C.2 D.2
答案:B
解析:
根據(jù)直觀圖可得該幾何體的俯視圖是一個直角邊長分別是2和的直角三角形(如圖所示)��,根據(jù)三視圖可知該幾何體是一個三棱錐���,且三棱錐的高為3����,所以體積V=××3=.故選B.
11.
8、古人采用“用臼舂米”的方法脫去稻谷的外殼�,獲得可供食用的大米,用于舂米的“臼”多用石頭或木頭制成.一個“臼”的三視圖如圖所示���,則鑿去部分(看成一個簡單的組合體)的體積為( )
A.63π B.72π
C.79π D.99π
答案:A
解析:由三視圖得鑿去部分是圓柱與半球的組合體����,其中圓柱的高為5��,底面圓的半徑為3���,半球的半徑為3,所以組合體的體積為π×32×5+×π×33=63π.
12.已知三棱錐P-ABC的四個頂點都在球O的表面上�,PA⊥平面ABC,AB⊥BC����,且PA=8.若平面ABC截球O所得截面的面積為9π,則球O的表面積為( )
A.10π B.25π
C
9��、.50π D.100π
答案:D
解析:設(shè)球O的半徑為R���,由平面ABC截球O所得截面的面積為9π�����,得△ABC的外接圓的半徑為3.設(shè)該外接圓的圓心為D����,因為AB⊥BC,所以點D為AC的中點���,所以DC=3.因為PA⊥平面ABC���,易證PB⊥BC,所以PC為球O的直徑.又PA=8����,所以O(shè)D=PA=4,所以R=OC==5����,
所以球O的表面積為S=4πR2=100π.
二、填空題(本題共4小題���,每小題5分���,共20分)
13.[2019·長春市質(zhì)量監(jiān)測(一)]已知一所有棱長都是的三棱錐��,則該三棱錐的體積為________.
答案:
解析:記所有棱長都是的三棱錐為P-ABC�����,如圖所示�,取B
10�、C的中點O,連接AD�,PD,作PO⊥AD于點O����,則PO⊥平面ABC,且OP=×=�����,故三棱錐P-ABC的體積V=S△ABC·OP=××()2×=.
14.如圖�,在正三棱柱ABC-A1B1C1中�����,D為棱AA1的中點.若AA1=4�,AB=2��,則四棱錐B-ACC1D的體積為________.
答案:2
解析:取AC的中點O�����,連接BO(圖略)�,則BO⊥AC�,所以BO⊥平面ACC1D.
因為AB=2,所以BO=.
因為D為棱AA1的中點�,AA1=4,所以AD=2�,
所以S梯形ACC1D=×(2+4)×2=6,所以四棱錐B-ACC1D的體積為×6×=2.
15.如圖�����,半徑為4的球O中有一內(nèi)
11�、接圓柱,則圓柱的側(cè)面積最大值是________.
答案:32π
解析:設(shè)圓柱的上底面半徑為r�,球的半徑與上底面夾角為α,則r=4cos α��,圓柱的高為8sin α.
所以圓柱的側(cè)面積為32πsin 2α.
當(dāng)且僅當(dāng)α=時�,sin 2α=1,圓柱的側(cè)面積最大�,
所以圓柱的側(cè)面積的最大值為32π.
16.[2019·江西省五校協(xié)作體試題]某幾何體的三視圖如圖所示��,正視圖是一個上底為2��,下底為4的直角梯形����,俯視圖是一個邊長為4的等邊三角形��,則該幾何體的體積為____________.
答案:
解析:把三視圖還原成幾何體ABC-DEF�,如圖所示,在AD上取點G�����,使得AG=2�,連接GE,GF���,則把幾何體ABC-DEF分割成三棱柱ABC-GEF和三棱錐D-GEF��,所以VABC-DEF=VABC-GEF+VD-GEF=4×2+×4×2=.
8
 2020高考數(shù)學(xué)二輪復(fù)習(xí) 分層特訓(xùn)卷 客觀題專練 立體幾何(10) 文
2020高考數(shù)學(xué)二輪復(fù)習(xí) 分層特訓(xùn)卷 客觀題專練 立體幾何(10) 文