《2022年中考數(shù)學(xué)專題復(fù)習(xí) 分類練習(xí) 四邊形解答題》由會員分享，可在線閱讀，更多相關(guān)《2022年中考數(shù)學(xué)專題復(fù)習(xí) 分類練習(xí) 四邊形解答題（4頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、2022年中考數(shù)學(xué)專題復(fù)習(xí) 分類練習(xí) 四邊形解答題
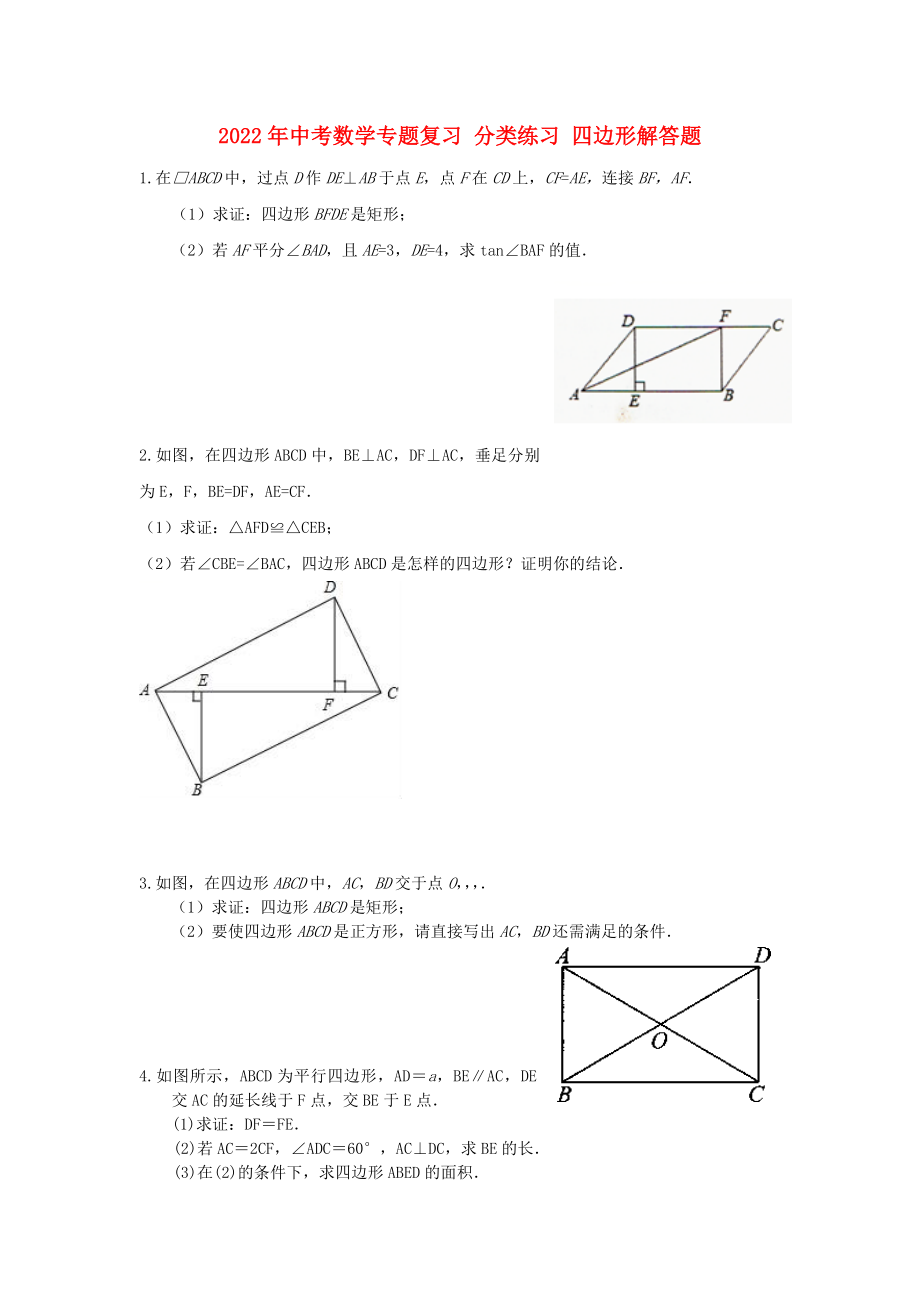
1.在□ABCD中，過點D作DE⊥AB于點E，點F在CD上，CF=AE，連接BF，AF．
（1）求證：四邊形BFDE是矩形；
（2）若AF平分∠BAD，且AE=3，DE=4，求tan∠BAF的值．
2.如圖，在四邊形ABCD中，BE⊥AC，DF⊥AC，垂足分別為E，F(xiàn)，BE=DF，AE=CF．
（1）求證：△AFD≌△CEB；
（2）若∠CBE=∠BAC，四邊形ABCD是怎樣的四邊形？證明你的結(jié)論．
3.如圖，在四邊形ABCD中，AC，BD交于點O，，，．
（1）求證：四邊形ABCD是矩形；
2、
（2）要使四邊形ABCD是正方形，請直接寫出AC，BD還需滿足的條件．
4.如圖所示，ABCD為平行四邊形，AD＝a，BE∥AC，DE交AC的延長線于F點，交BE于E點．
(1)求證：DF＝FE．
(2)若AC＝2CF，∠ADC＝60°，AC⊥DC，求BE的長．
(3)在(2)的條件下，求四邊形ABED的面積．
5.如圖所示，在直角梯形ABCD中，AD∥BC，AB⊥BC，∠DCB＝75°，以CD為一邊的等邊△DCE的另一頂點E在腰AB上．
(1)求∠AED的度數(shù)．
(2)求證：AB＝BC．
(3)若
3、F為線段CD上一點，∠FBC＝30°，求的值．
6.如圖，△ABC中，AB=AC=2，∠BAC=30°，△AEF是由△ABC繞點A按逆時針方向旋轉(zhuǎn)得到的，連接BE、CF相交于點D，是點B旋轉(zhuǎn)形成的?。?
（1）求證：BE=CF；
（2）當(dāng)四邊形ABDF為菱形時，求的長．
7.如圖，在菱形ABCD中，，點E在對角線BD上. 將線段CE繞點C順時針旋轉(zhuǎn)，得到CF，連接DF.
（1）求證：BE=DF；
（2）連接AC， 若EB=EC ，求證：.
8.如圖所示，點P位于等邊的內(nèi)部，且∠ACP=∠CBP．
(1) ∠BPC的度數(shù)
4、為________°；
(2) 延長BP至點D，使得PD=PC，連接AD，CD．
①依題意，補全圖形；
②證明：AD+CD=BD；
(3) 在(2)的條件下，若BD的長為2，求四邊形ABCD的面積．
9.如圖，在四邊形中，， 交于，是的中點，連接并延長，交于點，恰好是的中點.
（1）求的值；
（2）若，求證：四邊形是矩形.
10.如圖,在平行四邊形ABCD中,用直尺和圓規(guī)作∠BAD的平分線交BC于點E(尺規(guī)作圖的痕跡保留在圖中了),連接EF．
（1）求證：四邊形ABEF為菱形；
（2）AE，BF相交于點O，若BF=6，AB=5，求AE的長．
11.如圖，在菱形中，點、分別在邊、上,, 與相交于點.
(1) 求證: ;
(2) 當(dāng)時，求證:四邊形是平行四邊形.
12.己知：如圖，在菱形ABCD中，點E、F分別在邊BC、CD，
∠BAF=∠DAE，AE與BD交于點G．
（1）求證：BE=DF；
（2）當(dāng)=時，求證：四邊形BEFG是平行四邊形．
13.如圖，菱形的邊長為2，對角線，、分別是、上的兩個動點，且滿足.
(1)求證:;
(2)判斷的形狀，并說明理由，同時指出是由經(jīng)過如何變換得到.
2022年中考數(shù)學(xué)專題復(fù)習(xí) 分類練習(xí) 四邊形解答題
